チャート
移動平均 (MA)
移動平均は異なったサブセットの一連の平均を作成します。各新規のサブセットは、新規の値を追加して古い値を取り除くことで、一定の長さを保持します。移動平均は、N-期間のデータがユーザーに定義されます。他のテクニカル指標に加えこのテクニカル分析指標は、ユーザーが計算で使用する移動平均のタイプを選択できるようになっています。[数式] セクションには、各タイプの数式が表示されます。
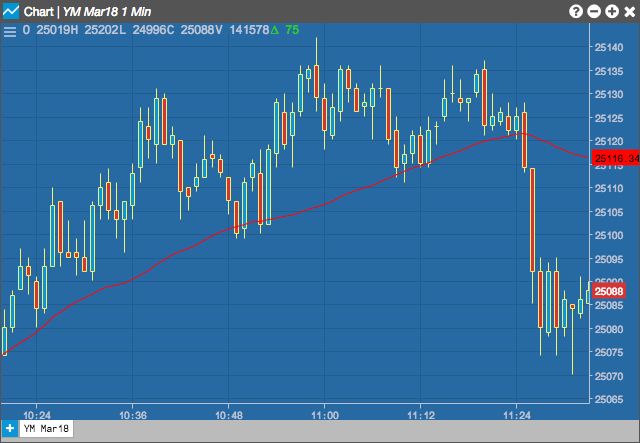
移動平均の方向 (高値、安値、フラット値) は、市場の動向を示し、スロープは動向の強さを示します。長期の平均は、より長期間の動向を識別するのに使用され、短期の平均は、より短期間の動向を識別するのに使用されます。
Configuration Options
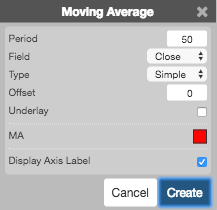
- Period (ピリオド): 計算で使用されるバー数。
- 欄: 平均計算のベースに使用する価格、または価格の組み合わせ。以下の値があります。
- Open (始値)
- High (高値)
- Low (安値)
- Close (終値)
- Adjusted Close (調整終値)
- HL/2 \( \left ( \frac{High + Low}{2} \right ) \)
- HLC/3 \( \left ( \frac{High + Low + Close}{3} \right ) \)
- HLCC/4 \( \left ( \frac{High + Low + Close + Close}{4} \right ) \)
- OHLC/4 \( \left ( \frac{Open + High + Low + Close}{4} \right ) \)
- Moving Average Type: Type of moving average to use in the calculations:
- Simple: Mean (average) of the data.
- Exponential: Newer data are weighted more heavily geometrically.
- Time Series: Calculates a linear regression trendline using the “least squares fit” method.
- Triangular: Weighted average where the middle data are given the most weight, decreasing linearly to the end points.
- Variable: An exponential moving average with a volatility index factored into the smoothing formula. The Variable Moving average uses the Chande Momentum Oscillator as the volatility index.
- VIDYA: An exponential moving average with a volatility index factored into the smoothing formula. The VIDYA moving average uses the Standard Deviation as the volatility index. (Volatility Index DYnamic Average).
- Weighted: Newer data are weighted more heavily arithmetically.
- Welles Winder:The standard exponential moving average formula converts the time period to a fraction using the formula EMA% = 2/(n + 1) where n is the number of days. For example, the EMA% for 14 days is 2/(14 days +1) = 13.3%. Wilder, however, uses an EMA% of 1/14 (1/n) which equals 7.1%. This equates to a 27-day exponential moving average using the standard formula.
- Hull: The Hull Moving Average makes a moving average more responsive while maintaining a curve smoothness. The formula for calculating this average is as follows: HMA[i] = MA( (2*MA(input, period/2) – MA(input, period)), SQRT(period)) where MA is a moving average and SQRT is square root.
- Double Exponential: The Double Exponential moving average attempts to remove the inherent lag associated to Moving Averages by placing more weight on recent values.
- Triple Exponential: TBD
- Simple
- Exponential
- Time Series
- Triangular
- Variable
- VIDYA
- Weighted
- Welles Winder
- Hull
- Double Exponential
- Triple Exponential
- タイプ: 移動平均のタイプ
- 単純移動平均 (Simple): データの平均。
- 指数移動平均 (Exponential)より新しいデータは、幾何学的により加重されています。
- 時系列 (Time Series): 「最小二乗法フィット」 を使って線形回帰動向を計算します。
- Triangular (三角形): 中央データにもっとも加重がおかれる加重平均で、最終点までの下降の線形です。
- 変数 (Variable): 平準化数式にボラティリティ指数が考慮された指数移動平均。変数移動平均 (Variable Moving average) は、ボラティリティ指数としてシャンデ・モメンタム・オシレーターを使用します。
- VIDYA: 平準化数式にボラティリティ指数が考慮された指数移動平均。VIDYA 移動平均 (VIDYA Moving average) は、ボラティリティ指数として標準偏差を使用します。(Volatility Index DYnamic Average).
- 加重平均価格指標 (Weighted): より新しいデータは、算術的により加重されています。
- ウェルズ・ワイルダー (Welles Wilder): 標準指数移動平均は、数式 EMA% = 2/(n + 1) を使って、時間の期間を分数に変換します。n は日数を示します。例えば、14日間の EMA% は 2/(14 日 +1) = 13.3% となります。ワイルダーは、1/14 (1/n) の EMA% で、7.1% を使用します。これは、標準の数式を使うと27日の指数移動平均と等しくなります。
- Hull
- 二重指数移動平均 (Double Exponential)
- 三重指数移動平均 (Triple Exponential)
- Offset (オフセット):
- Underlay: チャートの下に移動平均を表示するかどうか。
- Color Selectors (配色セレクター): グラフ要素に使用する配色。
- Display Axis Label (軸ラベルの表示): Y 軸に最新値を表示するかどうか。
数式
\[Simple = MA = \frac{\sum_{i=1}^{n} Close_{i}}{n}\]
\[Exponential = EMA = (Close_{n} - EMA_{t-1}) \times k + EMA_{n-1}\]
k = 平滑化定数、\( \frac{2}{n+1}\) と同等
n = 単純移動平均の期間数で、EMA によりほぼ近似
\[Time\;Series = TSMA = \frac{\sum_{i=1}^{n} Close_{i}}{n}\]
\[Triangular = TMA = \frac{\sum_{i=1}^{n} MA_{i}}{n} \]
where \(MA = \frac{\sum_{i=1}^{n} Close_{i}}{n} \)
\[Variable = VMA = \frac{P + (a \times b)P1 + {(a \times b)^2}P2 +...+{(a \times b)^{(n-1)}}P(n-1)}{1 + (a \times b) + (a \times b)^2 +...+ (a \times b)^{(n-1)}}\]
\[Weighted = WMA = \frac{n \times P + {(n-1) \times P1} + {(n-2) \times P2} +...+ P(n-1)}{1 + 2 +3 + ... +n}\]+n}\]
\[Welles\;Wilder Smoothing = WWS_{n} = WWS_{n-1} - \left ( \frac{WWS_{n-1}}{n} \right )+(Value_{n})\]
\( WWS_{1} = \frac{\sum_{i=1}^{n} Close_{i}}{n}\)\frac{\sum_{i=1}^{n} Close_{i}}{n}\)